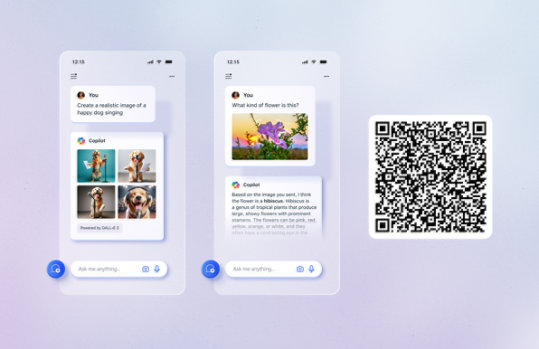
Unlock your potential with Microsoft Copilot
Get things done faster and unleash your creativity with the power of AI anywhere you go.
Visual Studio 2005 Retired documentation
PDF files that contain the Visual Studio 2005 documentation.
Important! Selecting a language below will dynamically change the complete page content to that language.
Version:
2005
Date Published:
9/21/2017
File Name:
VS2005_CPP_en-us.pdf
VS2005_CSharp_en-us.pdf
VS2005_DeviceDev_en-us.pdf
VS2005_General_en-us.pdf
VS2005_JScript_en-us.pdf
VS2005_JSharp_en-us.pdf
VS2005_SDK_en-us.pdf
VS2005_VB_en-us.pdf
VS2005_VSTO_en-us.pdf
VS2005_VWD_en-us.pdf
File Size:
104.1 MB
10.6 MB
3.2 MB
155.6 MB
3.3 MB
22.2 MB
232.8 MB
29.2 MB
94.4 MB
27.6 MB
PDF files that contain the Visual Studio 2005 documentation, formerly hosted online in MSDN under the Visual Studio 2005 node. This includes documentation for Visual Basic, C#, and Visual C++ as well as the Visual Studio documentation.Supported Operating Systems
Windows 2000 Service Pack 4, Windows Server 2003 Service Pack 1, Windows Vista, Windows XP Service Pack 2
A PDF viewer- The download contains several pdf files. To start the download, click Download.
- Select the files to download.
- Click Next
- If the File Download dialog box appears, do one of the following:
- To start the download immediately, click Open.
- To copy the download to your computer to view at a later time, click Save.
